Thời gian: 17-18/11/2023

Địa điểm: Đại Lải, Xuân Hòa, Hà Nội

Hình thức: Trực tiếp và trực tuyến:

Link theo dõi trực tuyến:

Join Zoom Meeting
https://us06web.zoom.us/j/89296705777?pwd=tcKTGKdpsFBnVD8WSvR804UsxwSj6g.1

Meeting ID: 892 9670 5777
Passcode: 123456

Chương trình:

Hodge theory in positive characteristic

Let 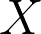be a proper and smooth scheme over a field k. The de Rham cohomology is the outcome of the Hodge spectral sequence

In characteristic 0 case, the sequence (1) degenerates at page . This is a very deep result in Hodge theory (when 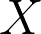is projective), and the proper case is reduced to the projective case by Chow lemma and a resolution of singularity (see [De68]).

In positive characteristic cases, things are more complicated. Mumford was the first one who gave a counter-example. On the other hand, Kato showed that if k is perfect and X is smooth projective over k, and assumes that there exists a lifting of 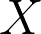on the Witt ring , then (1) degenerates.

The principal purpose of this workshop is to understand the paper of Deligne and Illusie [DI87] and of Ilusie [Il90], where the authors treated the above degenerating problem in a more general setting. That could be our first step in studying Hodge theory. Following is our detailed plan.

Talk 1: 17/11/2023; 14:00-15:15
Hodge spectral sequence in characteristic 0
Speaker: Nguyen The Hoang (Thang Long University)
Abstract: In this first talk, we will recall some results in Hodge theory in characteristic 0 case (references: [De68, Sec. 5] and [Ka70, Sec. 8]).

Talk 2: 17/11/2023; 15:30-16:45
Cartier isomorphism
Speaker: Pham Thanh Tam (Hanoi Pedagogical University 2)
Abstract: This talk introduces some basic tools to deal with Hodge spectral sequences in the case of positive characteristic: the Cartier isomorphism. Moreover, we also define Hodge filtration and introduce some essential concepts such as the Witt ring. (Reference: [Ca57] and [Ka70, Sec. 7]).

Talk 3: 17/11/2023; 17:00-18:15
Decomposition of de Rham complex
Speaker: Dang Quoc Huy (National Center for The- oretical Sciences, Taipei)
Abstract: This is one of the main results in [DI87]. After providing the decom- position, some applications to ”Hodge to de Rham” in characteristic 0 are also discussed. (Reference: [DI87, Sec. 2])

Talk 4: 18/11/2023; 8:00-9:15
Application to base change and finiteness theorems
Speaker: Dao Van Thinh (Institute of Mathematics)
Abstract: This talk gives some applications of the previous talk to characteristic p Hodge theory. We also discuss some variants in logarithmic cases. (References: [DI87, Sec. 4], and [EV86]).

Talk 5: 18/11/2023; 9:30-10:45
Decomposition of de Rham complex in relative case
Speaker: Tran Phan Quoc Bao (Institute of Mathematics)
Abstract: We follow Illusie to consider the relative case. To do so, we need to understand the setup: semi-stable reduction and relative Cartier isomorphism. Then we prove the decomposition theorem. (References: [Il90, Sec. 1 and 2]).

Talk 6: 18/11/2023; 11:00-12:15
The case with non-trivial coefficients
Speaker: Vo Quoc Bao (Institute of Mathematics)
Abstract: This talk generalizes further the above theory to the de Rham coho- mology with coefficients which are Gauss-Manin connections. (Reference: I90 [Il90, Sec. 3]).

References

• [Ca57] Cartier, P., Une nouvelle opération sur les formes différentielles. C. R. Acad. Sci., Paris, 244, 426-428 91957).
• [De68] Deligne, P., Théorème de Lefschetz et critères de dégénérescence de suites spectrales. Publ. Math., Inst. Hautes Etude Sci. 35, 107-126 (1968).
• [DI87] P. Deligne and L. Illusie, Relèvements modulo p2 et décomposition du complexe de de Rham, Inv. math. 89 (1987), 247-270.
• [EV86] H. Esnault and E. Viehweg, Logarithmic de Rham complexes and vanishing theorem, Inv. math. 86 (1986), 161-194.
• [Il90] Illusie, L., Reduction semi-stable et decomposition de complexes de de Rham a coefficients. Duke Math. Journal, vol. 60, no. 1 (1990).
• [Ka70] Katz, N., Nilpotent Connections and the Monodromy Theorem. Publ. Math., Inst. Hautes Etude Sci. 39, 175-232 (1970).