|
|
|
Recent
Issues
|
|
Volume 53
|
1
|
2
|
3
|
4
|
|
Volume 52
|
1
|
2
|
3
|
4
|
|
Volume 51
|
1
|
2
|
3
|
4
|
|
Volume 50
|
1
|
2
|
3
|
4
|
|
Volume 49
|
1
|
2
|
3
|
4
|
|
|
Vietnam Journal of Mathematics 39:3 (2011)
309-326
|
|
Higher Twists and Higher Gauss Sums
|
|
Siegfried Boecherer1 and
Alexei A. Panchishkin2
|
|
1Kunzenhof
4B, 79117 Freiburg, Germany
2Institut Fourier B.P.74, 38402 St.Martin
d’Hères, France
|
|
Abstract. We study two versions of higher twists of a Siegel modular form F
viewed as a formal Fourier expansion
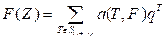
by a t-tuple ϕ of
Dirichlet characters ϕ = (ϕ1, …, ϕt) modulo N, where S(t+1)n denotes the set of
half-integral semi-positive symmetric matrices of size (t + 1)n × (t + 1)n. We show that both definitions are
related via shift matrix operators and higher Gauss sums. We establish a
spherical property of these higher Gauss sums (Proposition 2.1), and we
prove automorphy properties of the higher twists (Proposition 3.1 and Proposition
3.2). These twists belong to tensor products of certain spaces of modular
forms. This construction produces certain p-adic distributions with values in such tensor products
applicable in various constructions of p-adic L-functions.
|
|
|
|
Established
by Vietnam Academy of Science and Technology & Vietnam Mathematical
Society
Published
by Springer since January 2013
|
|