Home
Recent Issues
Volume 53	1
Volume 52	1	2	3	4
Volume 51	1	2	3	4
Volume 50	1	2	3	4
Volume 49	1	2	3	4
Past Issues
The Journal
Cover
Aims and Scope
Subscription Information
Editorial Board
Instructions for Author
Contact Us

Vietnam Journal of Mathematics 35:2(2007) 135-151

 Adjoint Line Bundles and Syzygies of Projective Varieties

Huy Tai Ha

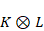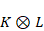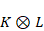Abstract.  Let X be a smooth projective variety and let K be the canonical divisor of X. In this paper, we study embeddings of X given by adjoint line bundles , where L is an ample invertible sheaf. When X is a regular surface and is normally generated (i.e. satisfies property N₀), we obtain a numerical criterion for to have property N_p. When X is a regular variety of arbitrary dimension, under a mild condition, we give an explicit calculation for the regularity of ideal sheaves of such embeddings.

2000 Mathematics Subject Classification: 14F17, 13D02, 14J60, 14C20.

Keywords: Adjoint line bundles, syzygies, minimal free resolution, Koszul cohomology.

Established by Vietnam Academy of Science and Technology & Vietnam Mathematical Society

Published by Springer since January 2013