Join Zoom Meeting
https://us06web.zoom.us/j/
Meeting ID: 876 7384 7104
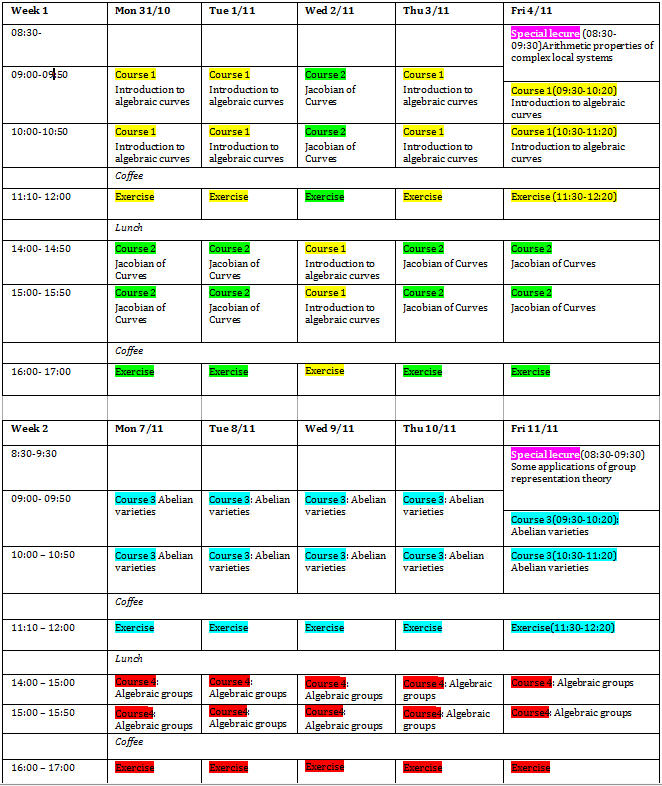
Special Lecture 1
Hélène Esnault
Arithmetic properties of complex local systems.
Abstract: We show some integrality properties of complex local systems on smooth complex quasi-projective varieties which are shown using arithmetic methods (Langlands program). In particular it yields an obstruction of a new kind for a finitely presented group to be the topological fundamental group of a smooth complex quasi-projective variety. (Work in progress with J. de Jong).
Special lecture 2
Phạm Hữu Tiệp
Some applications of group representation theory
Abstract: We will discuss how representation theory and group theory are used to resolve some problems motivated by applications in number theory and algebraic geometry.
Course 1: Introduction to algebraic curves
Đào Văn Thịnh;
This short course covers basic questions on algebraic curves. After some preliminaries, most of the rest of the course focuses on the Riemann-Roch theorem:
dim L(C,D)≥1−g(C)+degD,
where L(C,D) is the vector space of meromorphic functions on a non-singular projective algebraic curve C with poles bounded by a divisor D, and g(C) is the genus of C.
- Some basic concepts and theorems related to projective algebraic curves, main examples: plane curves
- Correspondence between function fields on one variable and nonsingular projective curves
- Rational functions and divisors on projective curves
- State and prove the Riemann-Roch theorem, present some of its applications
References
- William Fulton, Algebraic Curves: An Introduction to Algebraic Geometry online at www.math.lsa.umich.edu/~wfulton/CurveBook.pdf
- Robin Hartshorne, Algebraic Geometry, (Chapter 4 only)
- I.R. Shafarevich, Basic Algebraic Geometry (Part 1)
Course 2: Jacobian of Curves
Ngô Đắc Tuấn;
In this course we develop the algebraic theory of Jacobians for smooth projective curves. We present the construction, some basic properties and if time permits, we study the case of hyperelliptic curves.
- Divisors, lines bundles on curves.
- The Hilbert schemes of points. Symmetric powers.
- The Picard functor and the construction of Jacobians.
- The theta divisor and self-duality of Jacobians.
- Some examples.
References
- R. Hartshorne. Algebraic geometry. Graduate Texts in Mathematics, No. 52. Springer-Verlag, New York-Heidelberg, 1977.
- J. S. Milne. Abelian varieties. In Arithmetic geometry (Storrs, Conn., 1984), pages 103–150. Springer, New York, 1986.
Course 3: Abelian varieties
Joao Pedro dos Santos
- Rigidity lemma and applications: every morphism of abelian varieties is the composition of a group homomorphism and a translation, abelian varieties are commutative.
- Rational maps to abelian varieties,
- Theorem of the cube and applications, symmetric line bundles; projectivity of abelian varieties; structure of n-torsion subgroups. Isogenies.
- Quotients by finite groups: existence and basic properties of the quotient of a quasi-projective variety by a finite group.
References:
- Mumford, Abelian Varieties, Chapter II (+ Chapter III for the theorem of the cube)
- Milne, Abelian Varieties. https://www.jmilne.org/math/CourseNotes/AV.pdf
Course 4: Algebraic groups
Michel Brion
- Definitions and basic examples. Group actions, orbits, closed subgroups generated by images of morphisms.
- Structure of connected algebraic groups of dimension one via algebraic curves (this could give a nice application of the lectures on curves)
- The Albanese morphism
- Relation to the Jacobian.
- Statement of Chevalley's structure theorem
- Duality between the Picard and Albanese varieties.
- Statement of Chevalley's structure theorem: every connected algebraic group is an extension of an abelian variety by a connected linear group.
- Semi-abelian varieties and algebraically trivial line bundles on abelian varieties

